Hoe kan het verschil van twee kwadraten een derde macht opleveren? (ingediend door Hans Dijkstra)

Bij de lezing over getijdenkrachten van 25 november werd niet gerept over de precieze samenhang tussen de onderlinge afstand van hemellichamen en de getijdenkrachten die ze op elkaar uitoefenen. Uiteraard zijn de getijdenkracht kleiner als die afstand groter wordt. Getijdenkrachten zijn immers het verschil in aantrekkkingskracht tussen delen van een hemellichaam die naar een ander object toegewend zijn met delen die aan de andere, verre kant zitten. Wegens de zwaartekrachtwet van Newton zou je verwachten dat die krachten dus omgekeerd evenredig zijn met het kwadraat van de afstand. Wikipedia vertelt een ander verhaal. De getijdekracht is omgekeerd evenredig met de derdemacht van de afstand.
Hoe kan het verschil van twee kwadraten een derde macht opleveren?
Antwoorden van een wijze:
Piet Cijsouw MM 193 maart-augustus 2012

Vraag uit het vorige magazine:
Waarom neemt de getijdenkracht af met de derde macht van de afstand?
De redactie ontving drie antwoorden:
1:
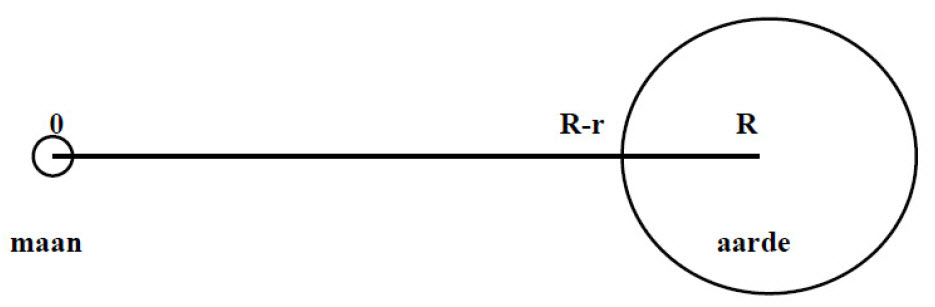
Waarom een derde macht? De aantrekkingskracht van de maan op een testmassa ter grootte 1 (kg) ergens op een afstand van R (meter) van de maan is G m / R2 , waar G de gravitatieconstante
van Newton is en m de massa van de maan (in kg). Die kracht is dus omgekeerd evenredig met het kwadraat van de afstand van de testmassa tot de maan, en hij is uiteraard op de maan gericht.
Neem nu de testmassa eerst in het punt aan het oppervlak van de aarde dat geheel aan de maanzijde ligt (vanaf de maan gezien dus de ʺvoorkantʺ van de aarde) en daarna in het middelpunt van de aarde
(in het laatste geval krijg je de gemiddelde kracht op een willekeurige massa ter grootte 1 op aarde). De eerste kracht is de grootste van de twee, omdat hij de kleinste afstand tot de maan heeft. De afstanden tot de
maan zijn resp. R – r en R, waar nu R de afstand aarde – maan is en r de straal van de aarde.
De aantrekkingskrachten zijn dus resp.
G m / (R – r)2 en G m / R2.
Het verschil tussen die twee krachten is de getijdenkracht: de extra aantrekkingskracht van de maan op een testmassa aan de ʺvoorkantʺ van de aarde, vergeleken met de ʺgemiddeldeʺ kracht.
Die extra kracht heeft blijkbaar als grootte (neem het verschilen breng alles op de noemer
R2 . (R –r)2)
G m [ R2 – (R-r)2 ] / [ R2 . (R–r)2 ] ofwel
G m r (2 R – r) / [ R2 . (R–r)2 ] .
Omdat r klein is ten opzichte van R kunnen we in de teller de factor 2R – r wel vervangen door 2R en in de noemer
R – r wel door R; dan komt er in benadering 2 G m r / R3
Een resultaat dus dat omgekeerd evenredig is met de derde macht van de afstand van de aarde tot de maan. De extra kracht is naar de maan gericht; dit levert de getijdenbult
aan de maanzijde van de aarde op. Op dezelfde manier vind je de extra kracht aan de ʺachterkantʺ van de aarde; die is even groot maar vande maan af gericht. Hij levert dus ook een getijdenbult op.
2: Hans Klein Woud MM 194 september-oktober 2012


3: Martin de Bogaerde MM 194 september-oktober 2012

Dit antwoord klopt wel maar de regel: Dit voldoet aan 4A3 + 27B2 ≠0 is overbodig en er wordt voorbijgegaan aan de context (getijdenwerking)
